Programming in Maxima
Lesson Maxima
Introduction
Maxima is a free computer algebra system (Computer algebra system — CAS), based on Common Lisp. In its functionality it is hardly inferior to other modern paid CAS, such as Mathcad, Mathematica, Maple; may conduct analytical (symbolic) calculations, numerical calculations, plot graphs (using gnuplot). There is a possibility of writing scripts, and even broadcast them in the code to Common Lisp and then compile it. In view of the fact that maxima was written from was developed by programmers of lisp, its syntax might seem a bit confusing, because the language is both imperative and functional. I will try to clarify these points and be able to present the essence of the functional approach and will not focus attention on specific mathematical functions: they are pretty easy to learn by yourself. This article discusses the peculiarities of calculation and syntax of maxima.
Shell
Of course, cause the maxima interpreter from the console is not very convenient. We want to look at the beautiful formulas, which are rendered with latex. So, for starters, I would suggest to put the shell wxMaxima. If you are fond of TeXmacs — you can configure it as a shell (to be honest, I have not tried). Well, for fans of emacs has imaxima, for work in the buffer. Is he literally out of the box.
Introduction
At first glance, everything is simple: enter an expression ending with a semicolon, we get the answer. Can try the maxima as a calculator, calculate the sum of the two numbers to calculate the sine of the angle, etc. go deeper what's going on.
Atoms
Symbols, numbers and Boolean constants true and false represent the simplest objects in the system. Of them lined up all the other expressions and the structure of the language, so they are called atomic (indivisible), or simply atoms.
Variables

In system are available and the above variables. The marked variables are bound variables, variables which are assigned some value. When interpreting the variable name is replaced by its value. Set variable using the ":". Free variables are not associated with any value and we can operate with them in the abstract, for example, to put two character expressions.
evaluation Context
When calculating each team formed its computational context. It is a set of relations between variable names and their values, as well as some parameters of interpretation. There are two computational context: local and global. The global context is common to all interpreted commands defines the current state of the interpreter. Local context is created while running a single command and are valid only for her. The most priority are the connections and settings on the local context.

Here, the value of a variable is taken from the global context, and for local installed option deployment works, that more works would not be deployed by themselves.
Block computations

Let's try to add two variables. Now we put to them the symbol in single quotes. It's operator lock computing. If we put it before the variable name — the result is the name of the variable before calling the function, the symbolic expression of a function call. Why? Sometimes you may need to use one function to handle an expression to another function and output a function or a number, for example calculation of indefinite integral. In other words, you have the opportunity to submit an expression as the data and manipulate with it. However, if you try to stop computing the sum of the two numbers, the calculation will not stop. This is due to the fact that the operator of the single quotes does not stop facilitation expressions (simple operations on numbers, reducing fractions). The same calculation will stop if you try to calculate the value of the function rational (float) argument.

Calculations
We learned that the interpreter distinguishes between the concept of symbolic expression, and calculate it. In some cases, there is a computation? The most obvious case is when we are trying to calculate what the expression (2+3, for example). Introduced the expression got its meaning. Considered a function of the argument — got value. Entered the name of the variable got its value. We learned that the value of the variable may be an atom, and symbolic expression. When there is a computation? The computation occurs while assigning a value to a variable. The value standing to the right of the colon is evaluated before assignment, so when assigning a character expression we quote that would stop the calculation. There is a special kind of assignment operator (two colons), when evaluated as an expression on the right, and the expression on the left. Also before the calculation of functions evaluate all arguments.

The result of a calculation variable a, variable b is on the left.
Example
Consider a simple example — the construction of the set of all subsets. As it turned out, the Maxima has built-in types for working with sets and such function, alas, no. Write it.
First, we understand that there are many. Apparently, many in the Maxima is based on another data structure — simply connected lists. What list understand everything. They have three main functions for working with them: the receipt of the item at the head of the list (first), get a list consisting of the original without the first element (rest), add a new item to the beginning (cons) and concatenating two lists (append). Similar functions exist in any implementation of lisp, but most often are called a bit different: car, cdr, cons, append, respectively.
How do you usually imagined algorithm for solving this problem? It would be possible to present a subset in the feature vector and go through them all. However, we show what a functional approach. It is easy to see that each element is included in exactly half of the subsets. This simple fact is enough to build a recursive algorithm. Discard one element a from set A. the set of all subsets of A will consist of unions of all subsets of A\a and the set of all subsets of A\a, where each element a added. Using the last assertion can be any recursively to reduce the dimensionality of the problem, reducing it to a trivial case. For the implementation we need an additional function from two parameters (item and many sets), which would add the specified element in each set.

Note that the function Declaration is almost as in math. You should note that when determining the right part after the equal sign is not evaluated. (In order to define a function so that its definition is evaluated, you must use the form of define). There is a new computing form if. It works the same way as in imperative languages. If the condition evaluates the expression after then, when a failure — after else. Now we write the desired function.
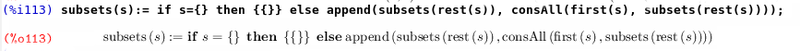
Let's try something to figure it out.

End
Well, that's all. In the following article it would be nice to describe the speedy implementation of the gradient descent.
Комментарии
Отправить комментарий